A commonly used measure of dispersion is the standard deviation, which is simply the square root of the variance. The variance of a data set is calculated by taking the arithmetic mean of the squared differences between each value and the mean value. Squaring the difference has at least three advantages:

1. Squaring makes each term positive so that values above the mean do not cancel values below the mean.

2. Squaring adds more weighting to the larger differences, and in many cases this extra weighting is appropriate since points further from the mean may be more significant.

3. The mathematics are relatively manageable when using this measure in subsequent statisitical calculations.

Because the differences are squared, the units of variance are not the same as the units of the data. Therefore, the standard deviation is reported as the square root of the variance and the units then correspond to those of the data set.

The calculation and notation of the variance and standard deviation depends on whether we are considering the entire population or a sample set. Following the general convention of using Greek characters to express population parameters and Arabic characters to express sample statistics, the notation for standard deviation and variance is as follows:

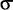  =  population standard deviation

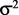  =  population variance

s  =  estimate of population standard deviation based on sampled data

s²  =  estimate of population variance based on sampled data

The population variance is defined as:

=

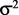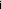The population standard deviation is the square root of this value.

The variance of a sampled subset of observations is calculated in a similar manner, using the appropriate notation for sample mean and number of observations. However, while the sample mean is an unbiased estimator of the population mean, the same is not true for the sample variance if it is calculated in the same manner as the population variance. If one took all possible samples of n members and calculated the sample variance of each combination using n in the denominator and averaged the results, the value would not be equal to the true value of the population variance; that is, it would be biased. This bias can be corrected by using ( n - 1 ) in the denominator instead of just n, in which case the sample variance becomes an unbiased estimator of the population variance.

This corrected sample variance is defined as:

s2    =

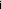The sample standard deviation is the square root of this value.

Standard deviation and variance are commonly used measures of dispersion. Additional measures include the range and average deviation.

Recommended Reading

Schaum's Outline of Statistics  - From the Schaum's Outline Series